Теория нечеткой логики впервые была рассмотрена в работах Лотфи А. Задэ, профессора Калифорнийского университета в Беркли в 1965 г. Несмотря на то, что математический аппарат нечеткой логики был разработан в США, активное развитие данного метода началось в Японии, и новая волна вновь достигла США и Европы. Основной причиной появления новой теории стало наличие нечетких и приближенных рассуждений при описании человеком процессов, систем, объектов.
Нечеткая логика является многозначной логикой, что позволяет определить промежуточные значения для оценок да/нет, истинно/ложно и т. д. Выражения подобные таким, как «слегка тепло» или «довольно холодно» возможно формулировать математически и обрабатывать на компьютерах.
Лингвистическая переменная – дистанция, температура, ошибка отклонения, производная ошибки отклонения, давление и т.д.
Терм – значение лингвистической переменной, выраженное словами естественного языка. Число термов выбирается из условия точности описания от трех и более. Например, 7:
– ошибка положительная большая (ПБ);
– ошибка положительная средняя (ПС);
– ошибка положительная малая (ПМ);
– ошибка близка к нулю (Н);
– ошибка отрицательная малая (ОМ);
– ошибка отрицательная средняя (ОС);
– ошибка отрицательная большая (ОБ).
Число 7 обусловлено емкостью кратковременной памяти человека, в которой, по современным представлениям, может храниться до семи единиц информации.
Понимание нечёткого управления можно получить через теорию нечётких множеств. Лингвистические переменные дают возможность применять математический аппарат к исходным данным, которые заданы неточно и если допускается результат невысокой точности.
Функция принадлежности – характеристическая функция, а ее значения mА(х) называется степенью принадлежности переменной х нечеткому множеству А и определяет соответствие числа между 1 и 0 данному значению физической величины (ФВ). Например: лингвистической переменной «ДИСТАНЦИЯ» для расстояния в 50 м можно задать степень принадлежности к терму «ДАЛЕКО», равную 0,85, а к терму «БЛИЗКО» – 0,15. Характеры функций принадлежности приведены на рис. 1: Z-функция, П-функция; Л-функция; S-функция. Выбор конкретной функции принадлежности осуществляется экспертами или экспертными системами.
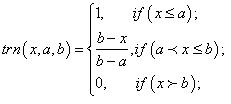
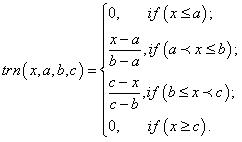
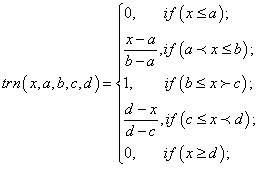
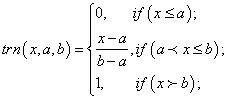
Рис. 1. Характеры функции принадлежности
Фаззификация – переход к нечеткости. Фаззификатор преобразует четкие входные сигналы, после их нормализации в относительный диапазон изменения –1, 0, +1, в термы, например: ОБ, ОС, ОМ, Н, ПМ, ПС, ПБ.
Дефаззификация – устранение нечеткости. Дефаззификатор преобразует нечеткие значения величин к определенным физическим параметрам которые служат командами исполнительному устройству.
Контроллер нечеткой логики отличается от обычных контроллеров тем, что для описания системы используются знания экспертов вместо дифференциальных уравнений.
База знаний (БЗ) включает в себя продукционные правила, связывающие лингвистические переменные. БЗ формируется на стадии проектирования нечеткого регулятора на основе знаний о свойствах объекта управления по следующей технологии: задается цель управления и при выделении существенных и отсечении второстепенных факторов определяется начальное состояние системы, ее желаемое конечное состояние и правила действий, переводящее систему в желаемое конечное состояние.
На рис. 3 и рис. 4 показаны термы, соответственно, фаззификация ошибки и производной ошибки.
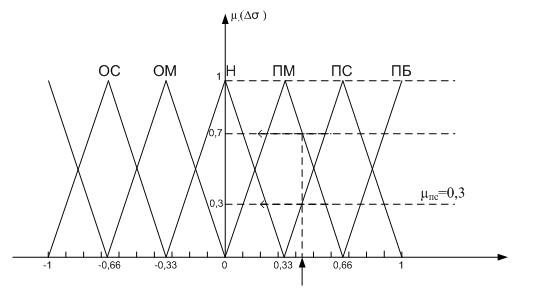
Рис. 3. Фаззификация ошибки
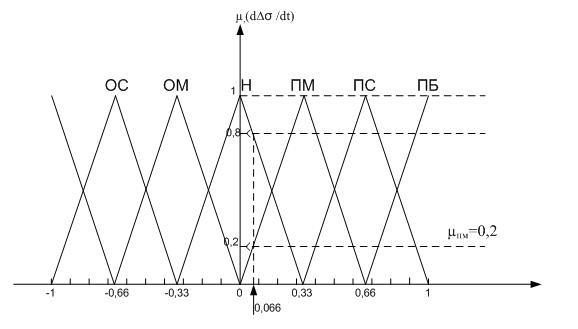
Рис. 4. Фаззификация производной ошибки
Формирование матрицы решений (7 7), которая приведена в табл. 1, выполнялось по следующим рассуждениям эксперта.
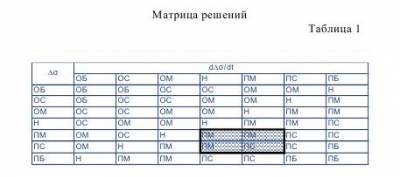
Матрица решений
Если ошибка большая (ПБ или ОБ) и скорость ее изменения большая и того же знака, то решение (управляющее воздействие) должно быть большим и того же знака, т.е. соответственно, ПБ или ОБ.
Если ошибка большая (ПБ или ОБ) и скорость ее изменения большая, но другого знака, то решение должно быть нулевым, так как ошибка быстро уменьшается.
Так, например, для изображенного на рис. 3 фаззификатора ошибки, четкое значение ошибки в 0,44 имеет нечеткие значения в виде терма ПС со степенью принадлежности 0,3 и терма ПМ со степенью принадлежности 0,7. Аналогично фаззифицируется и производная ошибки и при той же структуре фаззификатора при четком значении производной ошибки в 0,066 будем иметь нечеткие значения в виде терма ПМ со степенью принадлежности 0,2 и терма Н со степенью принадлежности 0,8. Остальные термы имеют степень принадлежности равную 0.
В матрице решений (табл.1) окаймлены четыре правила для нахождения нечеткого значения выходной переменной.
Первое правило: если Ds = ПМ и 
= Н, то a = ПМ. Степень принадлежности выходного терма ПМ
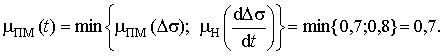
Второе правило: если Ds = ПМ и 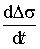= Н, то a = ПМ. Степень принадлежности выходного терма ПМ
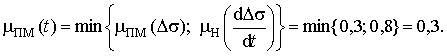
Третье правило: если Ds = ПМ и 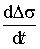= ПМ, то a = Пм. Степень принадлежности выходного терма ПМ
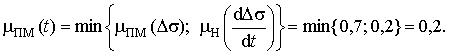
Четвертое правило: если Ds = ПС и 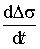= ПМ, то a = ПС. Степень принадлежности выходного терма ПС
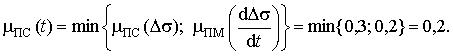
Далее для формирования нечеткого вывода определим степень принадлежности термов выходной переменной по максимуму. Так как терм ПМ имеет разные значения, то берем максимум
Таким образом, при данном состоянии входных сигналов степени принадлежности термов выходной переменной μ имеют значения
Заключительная операция в работе нечеткого регулятора переводит полученное результирующее нечеткое множество выходной переменной регулятора в четкое ее значение для управления. Устранение нечеткости окончательного результата (деффазификация), показанной на рис. 5, выполним методом полной интерпретации (вычислением координаты «центра тяжести» функции принадлежности на оси абсцисс).
Запишем формулу дефаззификации по методу центра тяжести (полная интерпретация)
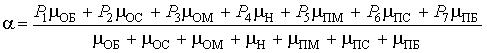
Подставив в формулу численные значения степеней принадлежности выходной переменной, получим:
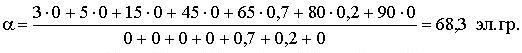
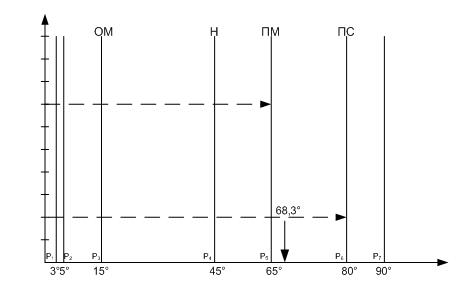
Рис. 5. Деффазификация управления
На рис. 6 приведено графическое представление инференц-механиз-ма дефаззификации.
Таким образом, рассчитано управляющее воздействие m (угол открытия a управляемого выпрямителя).
Порядок проектирования фаззи-регулятора
- Задать цель проектирования.
- Составить структурную схему САР.
- Выбрать лингвистические переменные и задать их характер.
- Задать число терм по каждой функции принадлежности.
- Задать под диапазоны лингвистических переменных.
- Составить матрицу решений базы знаний с помощью экспертов по схеме логической импликации ЕСЛИ-ТО.
- Задать правила работы механизма вывода решений (дефаззификатора).
- Выбрать логический контроллер.
Достоинства нечеткой логики
- Возможность описания ассоциативного мышления человека.
- Возможность развития экспертных систем, которые способны аккумулировать знания, полученные человеком в различных областях деятельности.
- Позволяет работать с системами с неполной информацией либо с переменными параметрами высокой сложности через использование искусственных нейронных сетей.
- Сокращает трудо затраты на разработку прикладного программного обеспечения в среднем в 3 раза.
- Не требует математического описания элементов САР.
- Пригодна для автоматизации нелинейных систем высоких порядков.
- Принципы построения управляющих программ позволяют легко работать с ними оператору, не знающему программирования.
- Дает возможность построения систем с нечеткой динамической коррекцией параметров традиционных регуляторов.
- Позволяет получить качественный переходный процесс без использования громоздких вычислительных процедур, характерных для классического метода управления с использованием принципа максимума.
Рис. 6. Графическое представление инференц-механизма дефаззификации.
Статья в pdf:Fuzzy logic
программа регулятора: